turunan fungsi implisit dan turunan logaritma
TURUNAN
Definisi Turunan Fungsi Implisit yaitu fungsi yang memuat dua variabel atau lebih, variabel-variabel tersebut terdiri dari variabel bebas dan variabel tidak bebas, biasanya variabel-variabel tersebut dinyatakan dalam x dan y dimana variabel x dan y terletak didalam satu ruas sehingga tidak dapat dipisahkan menjadi ruas yang berbeda (baca : ruas kiri dan ruas kanan) seperti halnya fungsi eksplisit. |
Turunan Fungsi Implisit Serta bentuk umum nya
Secara umum bentuk turunan fungsi implisit adalah f(x,y) = 0, mencari turunan fungsi implisit sama dengan mencari solusi bentuk umumnya dan prinsipnya tidak jauh berbeda dengan mencari turunan fungsi biasa.
Untuk lebih jelasnya Perhatikan contoh-contoh soal dibawah ini, bagaimana mencari turunan fungsi implisit.
Contoh :
Tentukan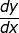 
dari setiap fungsi Implisit dibawah ini!
dari setiap fungsi Implisit dibawah ini!
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[Penyelesaian]
Turunkanlah kedua ruas terhadap x,
[penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
[Penyelesaian]
Turunkanlah kedua ruas terhadap x
Beberapa kasus dapat diselesaikan dengan 2 cara yaitu:
Cara I :
x3-3x2y+y2=0
3x2-6xy-3x2dydx+2ydydx=0
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
Cara II:
x3-3x2y+y2=0
3x2dx-6xy dx-3x2dy+2y dy=03x2-6xy-3x2dydx+2ydydx=0:dx
dydx(-3x2+2y)=-3x2+6xy
dydx=-3x2+6xy-3x2+2y
2. Turunan Logaritma
Katakanlah semisal kita memiliki fungsi f(x) =5log(x3+x2-4) maka bagaimanakah kita menemukan turunan dari fungsi tersebut?
Sebelum kita menginjak ke contoh tersebut, marilah kita uraikan dahulu fungsi logaritma yang paling sederhana, yaitu: f(x) = a log x.
Sebelum kita mengetahui turunan nya mari kita lihat sifat-sifat dan rumus-rumus logaritma :
Berikut adalah rumus-rumus dasar turunan/ derivatif:
Bila y=f(x) , y’=f’(x), dan a adalah konstanta maka:
| _ |
|
turunan logaritma sangat erat kaitannya dengan logaritma natural :
Sifat-sifat Logaritma |
ª log a = 1 |
ª log 1 = 0 |
ª log aⁿ = n |
ª log bⁿ = n • ª log b |
ª log b • c = ª log b + ª log c |
ª log b/c = ª log b – ª log c |
ªˆⁿ log b m = m/n • ª log b |
ª log b = 1 ÷ b log a |
ª log b • b log c • c log d = ª log d |
ª log b = c log b ÷ c log a |
Jika diketahui f(x) = a log x, maka,
Untuk f(x) =5log(x3+x2-4),
maka a=5, g(x)= x3+x2-4, dan g’(x)=3 x2+2x.
Sehingga turunan dari f(x) =5log(x3+x2-4) adalah
Agar lebih jelas perhatikan contoh soal berikut
Contoh 1 :
Tentukan turunan pertama dari y = ln (8x +1)
Jawab :
Tentukan turunan pertama dari y = ln (8x +1)
Jawab :
Contoh 2 :
Tentukan turunan pertama dari y = ln 9x adalah ....
Jawab :
Cara I :
Tentukan turunan pertama dari y = ln 9x adalah ....
Jawab :
Cara I :
Cara II
y = ln 9x = ln 9 + ln x
y = ln 9x = ln 9 + ln x
Maka :
(ln 9 adalah konstanta, jadi turunannya = 0)
(ln 9 adalah konstanta, jadi turunannya = 0)
Contoh 3 :
Turunan pertama dari y = ln sin x adalah ...
Jawab :
Contoh 4 :
Turunan pertama dari y = ln cos x adalah ...
Jawab :
Turunan pertama dari y = ln sin x adalah ...
Jawab :
Contoh 4 :
Turunan pertama dari y = ln cos x adalah ...
Jawab :
Contoh 5 :
f (x) = 7log x maka f ‘(x) = …
Jawab :
Adapun beberapa soal yg di jawab menggunakan metode rumus yg berbeda. Untuk lebih lengkap nya lihat contoh berikut :
Tentukan turunan fungsi-fungsi berikut ini!
1. 
[Penyelesaian]
2.
[Penyelesaian]
3. 
[Penyelesaian]
4. 
[Penyelesaian]
Comments
Post a Comment